The price function of a European call option under stochastic interest rates can also be solved using
Question:
The price function of a European call option under stochastic interest rates can also be solved using the partial differential equation approach. Let the asset value process St and the short rate process rt be governed by
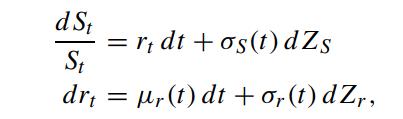 where dZS dZr = ρdt. Let λr denote the market price of risk of the short rate. Let c(S,r,t) denote the time-t value of a European call option with strike price X and maturity date T.
where dZS dZr = ρdt. Let λr denote the market price of risk of the short rate. Let c(S,r,t) denote the time-t value of a European call option with strike price X and maturity date T.
(a) Show that the governing equation c(S,r,t) is given by
![o3(t) 03(t) $202c t 2 2 S2 + + rS- as + pos(t)a, (t)S: + [ur(t) 2,o,(1)] r 22c asar - + - rc = 0). of (t)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/6/3/3/813655d9cd5332c61700633812524.jpg)
(b) Let B(r,t; T) denote the discount bond price, which satisfies
![a B + at o? (t) 02 2 ar2 + [ur(t) 2,5,(t)]B - r B = 0.](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/6/3/3/841655d9cf11d4951700633840697.jpg)
The bond price function admits a solution of the form
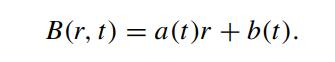
Defining ξ = S/B and u = c/B, show that u(ξ,t) satisfies
![t + (1) [ 2 post)ort)a(1) + a?(that)], du -2 2 d2 = 0.](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/6/3/3/909655d9d35df8211700633909419.jpg)
(c) Show that the value of the European equity call option under stochastic interest rates is given by
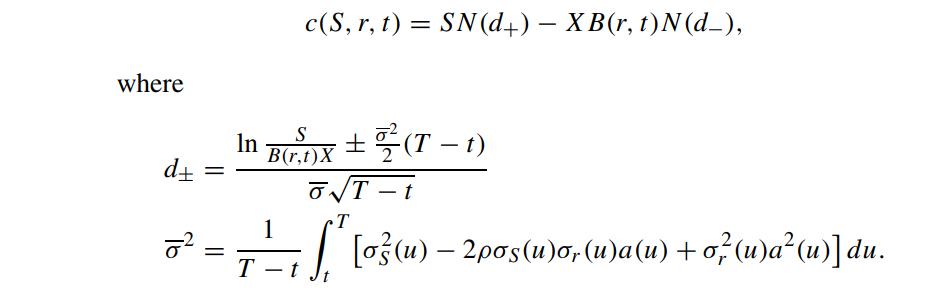
Step by Step Answer:






