We can also derive the binomial formula using the riskless hedging principle (see Sect. 3.1.1). Suppose we
Question:
We can also derive the binomial formula using the riskless hedging principle (see Sect. 3.1.1). Suppose we have a call that is one period from expiry and we would like to create a perfectly hedged portfolio with a long position of one unit of the underlying asset and a short position of m units of call. Let cu and cd denote the payoff of the call at expiry corresponding to the upward and downward movement of the asset price, respectively. Show that the number of calls to be sold short in the portfolio should be
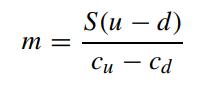
in order that the portfolio is perfectly hedged. The hedged portfolio should earn the risk-free interest rate. Let R denote the growth factor of a perfectly hedged riskfree portfolio over one period. Show that the binomial option pricing formula for the call as deduced from the riskless hedging principle is given by
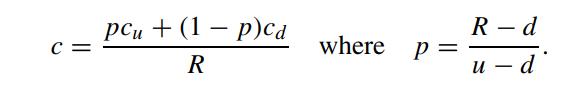
Step by Step Answer:






