We define the geometric average of the price path of asset price S i , i =
Question:
We define the geometric average of the price path of asset price Si, i = 1, 2, during the time interval [t,t + T ] by
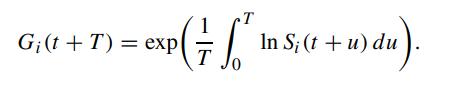
Consider an Asian option involving two assets whose terminal payoff is given by max(G1(t+T )−G2(t+T ), 0). Show that the price formula of this European Asian option at time t is given by (Boyle, 1993)
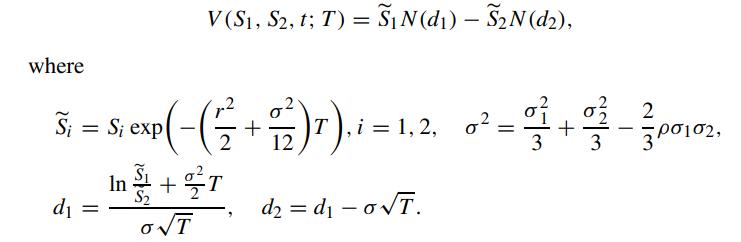
Apply the price formula of the exchange option in Problem 3.34.
Problem 3.34.
Consider the exchange option that gives the holder the right but not the obligation to exchange risky asset S2 for another risky asset S1. Let the price dynamics of S1 and S2 under the risk neutral measure be governed by
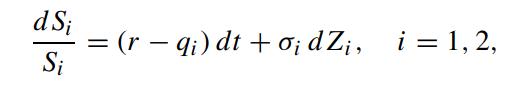
where dZ1 dZ2 = ρdt. Let V (S1,S2,τ) denote the price function of the exchange option, whose terminal payoff takes the form
![]()
Show that the governing equation for V (S1,S2,τ) is given by
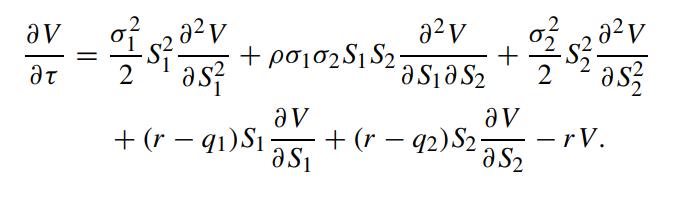 By taking S2 as the numeraire and defining the similarity variables:
By taking S2 as the numeraire and defining the similarity variables:
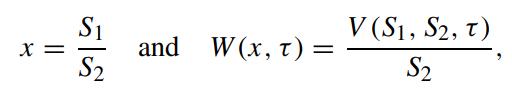
show that the governing equation for W(x,τ) becomes
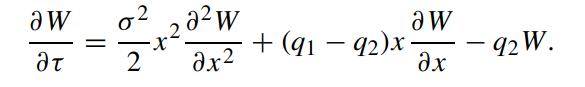 Verify that the solution to W(x,τ) is given by
Verify that the solution to W(x,τ) is given by
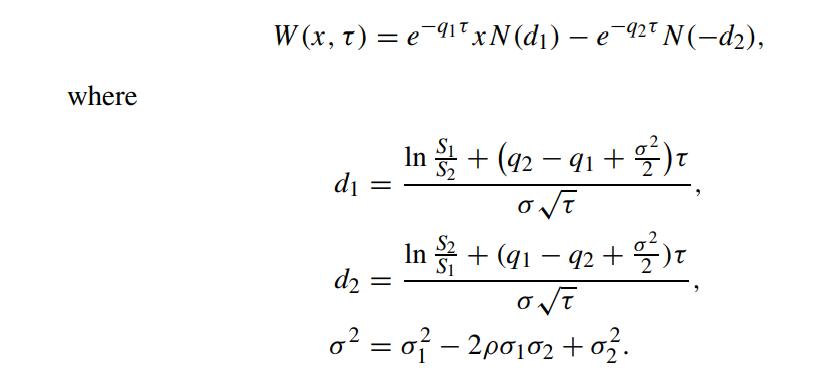
Referring to the original option price function V (S1,S2,τ), we obtain
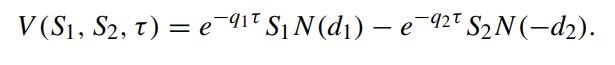
Step by Step Answer:






