In Example 2B we saw that there was no optimal solution for the problem of maximizing the
Question:
In Example 2B we saw that there was no optimal solution for the problem of maximizing the objective function z over the feasible region S. We want to add an additional constraint to modify the feasible region so that an optimal solution for the maximization problem does exist. Which of the following constraints will accomplish this objective?
(A) x ≤ 20
(B) y ≥ 4
(C) x ≤ y
(D) y ≤ x
Example 2B
Minimize and maximize subject to
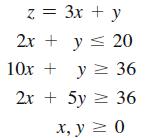
Minimize and maximize subject to
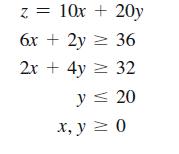
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Finite Mathematics For Business Economics Life Sciences And Social Sciences
ISBN: 9780134862620
14th Edition
Authors: Raymond Barnett, Michael Ziegler, Karl Byleen, Christopher Stocker
Question Posted:





