Let (A) Show that if the row minima belong to the same column, at least one of

Question:

Let

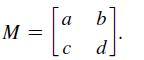
M = LC b d

(A) Show that if the row minima belong to the same column, at least one of them is a saddle value.

(B) Show that if the column maxima belong to the same row, at least one of them is a saddle value.

(D) Explain why part (C) implies that the denominator D in Theorem 4 will never be 0.

Data from Theorem 4

THEOREM 4 Solution to a 2 x 2 Nonstrictly Determined Matrix Game For the nonstrictly determined game a b d

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Finite Mathematics For Business Economics Life Sciences And Social Sciences

ISBN: 9780134862620

14th Edition

Authors: Raymond Barnett, Michael Ziegler, Karl Byleen, Christopher Stocker

See More Books

Question Posted: Dec 29, 2023 07:00 AM

See More Questions

The Smiths have two children. At least one of them is a boy. What is the probability that both children are boys? (See Gardner 1961 for a complete discussion of this problem.)
You are a partner at ABC CPA, and you are auditing December 31, 2020 financial statements of FlyPlane. FlyPlane is an airline in Canada and is a private company. You were hired to do this audit in...
36. Let I = = (x 3y + 1) dx + (ye* + y) dy, where C is the trapezoid in the xy-plane with vertices (0,0), (2,0), (2,1), and (1,1) oriented 1 counter-clockwise. Find the value of I.
Write a Summary of Tartuffe the Norton anthology of western literature.
A ball initially slides without rotating on a horizontal surface with friction (see Fig). The initial speed of the ball is V0, and the moment of inertia about its center is I = ?mR2.(a) Without...
How could SDI reduce the likelihood of similar lawsuits occurring in the future? Aegis Communications hired Southwest Desert Images, LLC, (SDI) to provide landscaping services for its property. SDI...
Consider a dataset consisting of 20 observations with the following summary statistics: $\bar{x}=0, \bar{y}=9, s_{x}=1$, and $s_{y}=10$. You run a regression using using one variable and...
The McCoy Family raises cattle on their farm in Virginia. They also have a large garden in which they grow ingredients for making two types of relishchow-chow and tomato. These they sell in 16-ounce...
Consider the recorded transactions below. Transaction Account Name Debit Credit 1. Accounts Receivable 7,400 Service Revenue 7,400 2. Supplies 1,800 Accounts Payable 1,800 3. Cash 9,200 Accounts...
A simply supported pretensioned beam has a span of 75 ft (22.9 m) and the cross section shown in Figure P3.1. It is subjected to a uniform gravitational live-load intensity W =1,200 plf (17.5 kN/m)...
In Problem solve each matrix game. [ 4 0 -1 2.
Outline a procedure for solving the 4 5 matrix game without actually solving the game. M = 2 -3 5 -4 -2 -1 6 -6 4 -1 6 0 2 7 3 63 - -7 4 -5
In this exercise, you modify one of the Projected Sales applications from this lesson. Use Windows to make a copy of the Sales Solution folder. Rename the copy Sales Solution-Intermediate. Open the...
A landlord appeals and a tenant cross-appeals a district court ruling affirming in part and reversing in part a small claims court decision in a residential landlordtenant dispute. This is a case...
In March 2014, Barbara Ann Morris executed an estate plan that designated her daughters, Karen Wyman and Pamala Bruckner, as the beneficiaries and Wyman as the personal representative of her estate....
The CCR Project is a forest management effort and timber sale affecting 11,742 acres in Mt. Hood National Forest. The United States Forest Service (USFS) undertook the CCR Project in order to provide...
Joseph Guenther and Michelle Ryerson were an unmarried couple. In June 2009, they purchased land in Idaho and formed a partnership to develop it into a profitable vineyard. There was no written...
Protect My Check, Inc. (PMC), is a Section 501(c)(4), an organization that must not be organized for profit and must be operated exclusively to promote social welfare. While it is based in Florida,...
It seems logical that restaurant chains with more units (restaurants) would have greater sales. This assumption is mitigated, however, by several possibilities: some units may be more profitable than...
Research an article from an online source, such as The Economist, Wall Street Journal, Journal of Economic Perspectives, American Journal of Agricultural Economics, or another academic journal. The...
Find a confidence interval for the slope that would describe the association between all hand spans and number of Tootsie Rolls grabbed. Is zero in this interval? Does this make sense based on the...
Are the validity conditions met to complete a theory-based t-test on these data? Explain. Whether the conditions are met or not, use a theory-based t-test to find a p-value. How does this p-value...
Use the appropriate applet to construct a simulated null distribution using the slope of the least squares regression line as the statistic. Mark the observed least squares slope on this graph. a....
Sales promotions At the bottom of all its February sales receipts, Seifert Stores Inc. printed $2-off coupons. The coupons may be redeemed March 1-April 30. Seifert Stores Inc. accepts only cash,...
Review of Uniqlo's Communication of Ethics and Approach to CSR and Sustainability in Relation of Ethical Marketing Strategies.
The costs per equivalent unit of direct materials and conversion in the Rolling Department of Jabari Steel Company are $375 and $60, respectively. The equivalent units to be assigned costs are as...

Let (A) Show that if the row minima belong to the same column, at least one of

Question:

M = LC b d

Step by Step Answer:

A To show that if the row minima belong to the same column at least one of them is a saddle value we ...View the full answer

Finite Mathematics For Business Economics Life Sciences And Social Sciences

Students also viewed these Mathematics questions