Let us return to Example 2, the tossing of a nickel and a dime, and the sample space

Since there are 4 simple outcomes and the coins are assumed to be fair, it would appear that each outcome would occur 25% of the time, in the long run. Let us assign the same probability of 14 to each simple event in S:

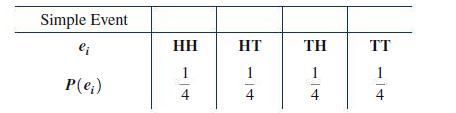
This is an acceptable assignment according to Conditions 1 and 2, and it is a reasonable assignment for ideal (perfectly balanced) coins or coins close to ideal.

(A) What is the probability of getting 1 head (and 1 tail)?

(B) What is the probability of getting at least 1 head?

(C) What is the probability of getting at least 1 head or at least 1 tail?

(D) What is the probability of getting 3 heads?

Data from Example 2

A nickel and a dime are tossed. How do we identify a sample space for this experiment? There are a number of possibilities, depending on our interest. We will consider three.

If we are interested in whether each coin falls heads (H) or tails (T), then, using a tree diagram, we can easily determine an appropriate sample space for the experiment:

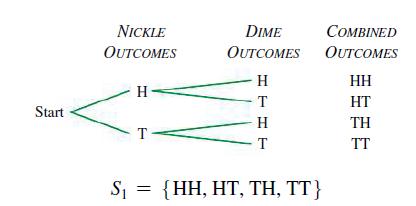
and there are 4 simple events in the sample space.

If we are interested only in the number of heads that appear on a single toss of the two coins, we can let

and there are 3 simple events in the sample space.

If we are interested in whether the coins match (M) or do not match (D), we can let

and there are only 2 simple events in the sample space.

Transcribed Image Text:

S = {HH, HT, TH, TT}