This is a continuation of Example 7 in Section 2.1. Recall that the financial department in the
Question:
This is a continuation of Example 7 in Section 2.1. Recall that the financial department in the company that produces a digital camera arrived at the following price–demand function and the corresponding revenue function:
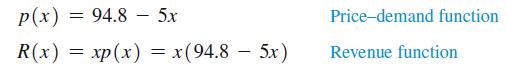
where p(x) is the wholesale price per camera at which x million cameras can be sold and R(x) is the corresponding revenue (in millions of dollars). Both functions have domain 1 ≤ x ≤ 15.
(A) Find the value of x to the nearest thousand cameras that will generate the maximum revenue. What is the maximum revenue to the nearest thousand dollars? Solve the problem algebraically by completing the square.
(B) What is the wholesale price per camera (to the nearest dollar) that generates the maximum revenue?
(C) Graph the revenue function using an appropriate viewing window.
(D) Find the value of x to the nearest thousand cameras that will generate the maximum revenue. What is the maximum revenue to the nearest thousand dollars? Solve the problem graphically using the maximum command.
Data from Example 7
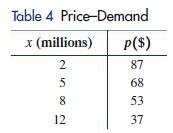
A manufacturer of a popular digital camera wholesales the camera to retail outlets throughout the United States. Using statistical methods, the financial department in the company produced the price–demand data in Table 4, where p is the wholesale price per camera at which x million cameras are sold. Notice that as the price goes down, the number sold goes up.
Using special analytical techniques (regression analysis), an analyst obtained the following price–demand function to model the Table 4 data:
![]()
Plot the data in Table 4. Then sketch a graph of the price–demand function in the same coordinate system.
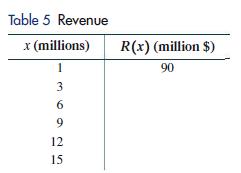
What is the company’s revenue function for this camera, and what is its domain?
Complete Table 5, computing revenues to the nearest million dollars.
Plot the data in Table 5. Then sketch a graph of the revenue function using these points.
Graph the revenue function on a graphing calculator.
Step by Step Answer:

Finite Mathematics For Business Economics Life Sciences And Social Sciences
ISBN: 9780134862620
14th Edition
Authors: Raymond Barnett, Michael Ziegler, Karl Byleen, Christopher Stocker





