For the system shown in Fig. 6.38, (a) determine the characteristic polynomial (Deltaleft(omega^{2} ight)=operatorname{det}left|[k]-omega^{2}[m] ight|), (b) plot (Deltaleft(omega^{2} ight)) from (omega^{2}=0) to (omega^{2}=4.0) (using increments

For the system shown in Fig. 6.38, (a) determine the characteristic polynomial \(\Delta\left(\omega^{2}\right)=\operatorname{det}\left|[k]-\omega^{2}[m]\right|\), (b) plot \(\Delta\left(\omega^{2}\right)\) from \(\omega^{2}=0\) to \(\omega^{2}=4.0\) (using increments \(\Delta \omega^{2}=0.2\) ), and (c) find \(\omega_{1}^{2}, \omega_{2}^{2}\), and \(\omega_{3}^{2}\).

Figure 6.38:-

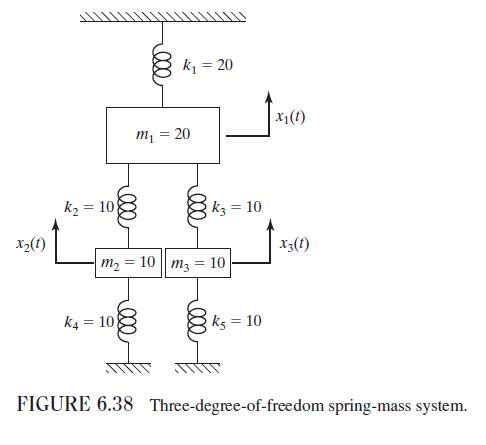
k =108 k = 20 m = 20 ,000. k = 10 x1(1) X2(1) X3(1) m2 = 10 m3 = 10 k4= 10 ks=10 FIGURE 6.38 Three-degree-of-freedom spring-mass system.