The differential equation of motion of an undamped system is given by (2 ddot{x}+150 x=F(t)) with the
Question:
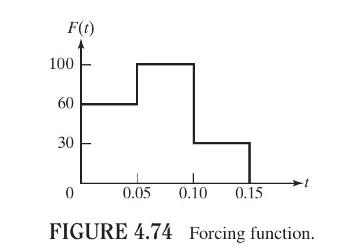
The differential equation of motion of an undamped system is given by \(2 \ddot{x}+150 x=F(t)\) with the initial conditions \(x_{0}=\dot{x}_{0}=0\). If \(F(t)\) is as shown in Fig. 4.74, find the response of the problem using the computer program of Problem 4.97.
Figure 4.74:-
Data From Problem 4.97:-
Write a MATLAB program for finding the steady-state response of a single-degree-of-freedom system subjected to an arbitrary force, by numerically evaluating the Duhamel integral. Using this program, solve Example 4.31.
Data From Example 4.31:-

Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





