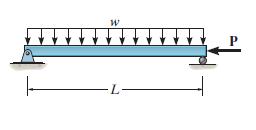
The ideal column has a weight \(w\) (force/length) and is subjected to the axial load \(\mathbf{P}\). Determine the maximum moment in the column at midspan. \(E I\) is constant. Establish the differential equation for deection, Eq. 13-1, with the origin at the midspan. The general solution is \(v=C_{1}\) \(\sin k x+C_{2} \cos k x+(w /(2 \mathrm{P})) x^{2}-(w L /(2 P)) x-\left(w E I / P^{2}\right)\) where \(k^{2}=P / E I\).

Transcribed Image Text:

-7-