Two circular aluminum pipes of equal length L = 24 in. are loaded by torsional moments T.
Question:
Two circular aluminum pipes of equal length L = 24 in. are loaded by torsional moments T. Pipe 1 has outside and inside diameters, d2 = 3 in. and d1 = 2.5 in, respectively. Pipe 2 has a constant outer diameter of d2 along its entire length and an inner diameter of d1 but has an increased inner diameter of d3 = 2.65 in. over the middle third. Assume that E = 10,400 ksi, y = 0.33, and allowable shear stress πa = 6500 psi.
(a) Find the maximum acceptable torques that can be applied to Pipe 1; repeat for Pipe 2.
(b) If the maximum twist f of Pipe 2 cannot exceed 5/4 of that of Pipe 1, what is the maximum acceptable length of the middle segment?
(c) Find the new value of inner diameter d3 of Pipe 2 if the maximum torque carried by Pipe 2 is to be 7/8 of that for Pipe 1.
(d) If the maximum normal strain in each pipe is known to εmax = 811 x 10-6, what is the applied torque on each pipe? Also, what is the maximum twist of each pipe? Use the original properties and dimensions.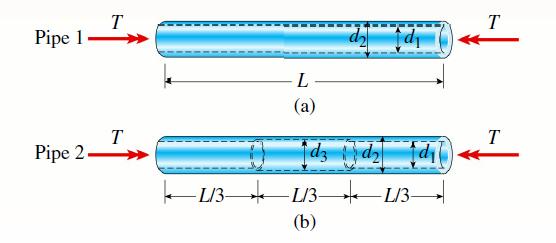
Step by Step Answer:






