A large number of particles, each of mass \(m\), move in response to a uniform gravitational field \(g\) in the negative \(z\) direction. At time \(t=0\), they are all located within the corners of a rectangle in \(\left(z, p_{z}\right)\) phase space, whose positions are: (1) \(z=z_{0}, p_{z}=p_{0}\), (2) \(z=z_{0}+\Delta z, p_{z}=p_{0}\), (3) \(z=z_{0}, p_{z}=p_{0}+\Delta p\), and (4) \(z=z_{0}+\Delta z, p_{z}=p_{0}+\Delta p\). By direct computation, find the area in phase space enclosed by these particles at times 

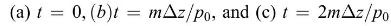
Also show the shape of the region in phase space for cases (b) and (c).

Transcribed Image Text:

(a) t = 0, (b)t = mAz/po, and (c) t = 2mAz/po.