A torus can be defined by two radii: A large radius (R) running around the center of
Question:
A torus can be defined by two radii: A large radius \(R\) running around the center of the torus, and a small radius \(r\) corresponding to a cross-sectional slice. Let \(R\) live in the \(x, y\) plane. Then if \(\varphi\) is an angle relative to the \(x\) axis and lying in the \(x, y\) plane, and \(\theta\) is an angle within a cross-sectional slice, with \(\theta=0\) corresponding to the outermost radius of the torus \(R+r\), then the Cartesian coordinates of points on the torus are
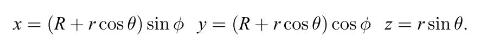

Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





