Consider the system shown in the figure below. The particle of mass \(m_{2}\) moves on a vertical axis without friction and the entire system rotates about this axis with a constant angular speed \(\Omega\). The frictionless joint near the top assures that the three masses always lie in the same plane; and the rods of length \(a\) are all rigid. (Use the origin of your coordinate system at the upper frictionless joint.)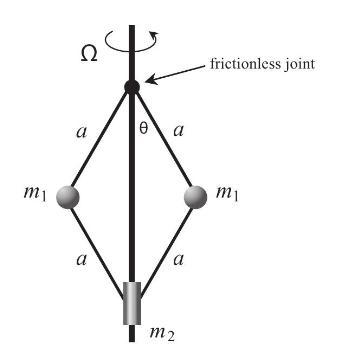

(a) Find the equation of motion in terms of the single degree of freedom \(\theta\).

(b) Using the method of Lagrange multipliers, find the torque on the masses \(m_{1}\) due to the rotational motion.

(c) Find a static solution in \(\theta\) and identify the corresponding angle in terms of \(m_{1}\), \(m_{2}, g, a\), and \(\Omega\). Consider some limits/inequalities in your result and comment on whether they make sense.

(d) Is the solution in part (c) stable? if so, what is the frequency of small oscillations about the configuration? (Use \(\xi=\cos \theta\) and work on the Lagrangian instead of the equation of motion.)

m1 a a a a Im 2 frictionless joint m1