In geometry, an ellipsoid constitutes the three-dimensional analogue of the ellipse in the plane. The equation of an ellipsoid in a Cartesian coordinate system is given by

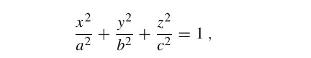
where \(a, b\) and \(c\) are fixed real numbers such that \(a \geq b \geq c>0\) represent the semi-axes of the ellipsoid. In the case of different \(a, b, c\), we have a scalene ellipsoid; if \(a>b=c\), we

have a prolate ellipsoid; in the case \(a=b>c\), we have a oblate ellipsoid. Without making use of integrals, but relying on the result of the question 13 show that the moment of inertia of a homogeneous ellipsoid of mass \(M\) with respect to the axis containing \(a\) is given by the relation \(J_{a}=\frac{M\left(b^{2}+c^{2}\right)}{5}\) and that similar relations hold for the moments of inertia with respect to the other axes \(b\left(J_{b}=\frac{M\left(a^{2}+c^{2}\right)}{5}\right)\) and \(c\left(J_{c}=\frac{M\left(a^{2}+b^{2}\right)}{5}\right)\).

Question 13

Using a spherical coordinate system, show that the moment of inertia of a solid sphere of radius \(R\) and mass \(M\) with respect to any diameter passing through the center is \(\frac{2}{5} M R^{2}\)

Transcribed Image Text:

= 22 + 26 +