Show that for the motion of a pendulum given by (4.40), the speed has maximum value in
Question:
Show that for the motion of a pendulum given by (4.40), the speed has maximum value in absolute value and negative sign at the time \(t=\pi / 2 \omega\). This causes the pendulum to continue motion in the negative-angle region. In contrast, the velocity has maximum (positive) value at time \(t=3 \pi / 2 \omega\). Remind you that motion in the absence of friction continues in the same way when the phase of the cosine function increases by a factor of \(2 \pi\).
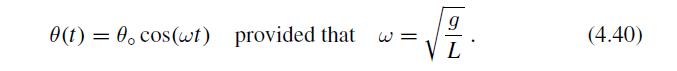
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





