Show that Maxwell's equations given by 8.16 imply the wave equations

\[abla^{2} \phi-\frac{1}{c^{2}} \frac{\partial^{2} \phi}{\partial t^{2}}=-4 \pi ho_{Q}\]

and

\[abla^{2} \mathbf{A}-\frac{1}{c^{2}} \frac{\partial^{2} \mathbf{A}}{\partial t^{2}}=-\frac{4 \pi}{c} \mathbf{J}\]

To do this, you will need the vector identity \(\boldsymbol{abla} \times \boldsymbol{abla} \times \mathbf{A}=\boldsymbol{abla}(\boldsymbol{abla} \cdot \mathbf{A})-abla^{2} \mathbf{A}\). You will also need to fix the gauge freedom using 

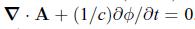
The latter is allowed due to the gauge symmetry discussed in the text.

Transcribed Image Text:

VA+(1/c)06/0t = 0.