The grand partition function of a gaseous system composed of mutually interacting bosons is given by [
Question:
The grand partition function of a gaseous system composed of mutually interacting bosons is given by
\[ \ln \mathcal{Q} \equiv \frac{P V}{k T}=\frac{V}{\lambda^{3}}\left[g_{5 / 2}(z)-2\left\{g_{3 / 2}(z)ight\}^{2} \frac{a}{\lambda}+O\left(\frac{a^{2}}{\lambda^{2}}ight)ight] \]
Study the analytic behavior of this expression near \(z=1\) and show that the system exhibits the phenomenon of Bose-Einstein condensation when its fugacity assumes the critical value
\[ z_{c}=1+4 \zeta\left(\frac{3}{2}ight) \frac{a}{\lambda_{c}}+O\left(\frac{a^{2}}{\lambda_{c}^{2}}ight) \]
Further show that the pressure of the gas at the critical point is given by (Lee and Yang 1958, 1960b)
\[ \frac{P_{c}}{k T_{c}}=\frac{1}{\lambda_{c}^{3}}\left[\zeta\left(\frac{5}{2}ight)+2\left\{\zeta\left(\frac{3}{2}ight)ight\}^{2} \frac{a}{\lambda_{c}}+O\left(\frac{a^{2}}{\lambda_{c}^{2}}ight)ight] \]
compare these results to equations (11.2.16) through (11.2.18).
Data From Equation (11.2.16) through (11.2.18)
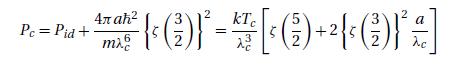
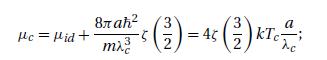
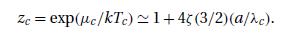
Step by Step Answer:






