The hidden symmetry of the previous few problems is part of a two-fold transformation - one of which is given by and another similar one that we have not shown; together, they result in the conservation of a vector known as the Laplace-RungeLenz vector

Show that Eq. 6.200 is the \(x\)-component of this more general vector quantity. (You may find it useful to use the identity \(\mathbf{a} \times(\mathbf{b} \times \mathbf{c})=\mathbf{b}(\mathbf{a} \cdot \mathbf{c})-\mathbf{c}(\mathbf{a} \cdot \mathbf{b}\).

Data from Eq. 6.200

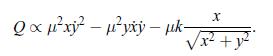
Data from Problem 6.16

The two-body central-force problem we have been dealing with in
the previous two problems also has another unexpected and amazing symmetry.
Consider the transformation

Transcribed Image Text:

Avx (rx pv) - k- = r