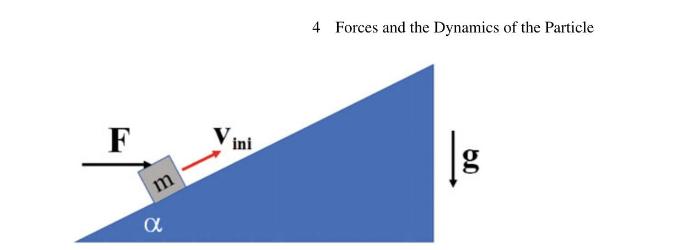
To a block of mass \(m=4.8 \mathrm{~kg}\) that is on an inclined plane at an angle \(\alpha=38^{\circ}\) to the horizontal, is applied the horizontal force, drawn in Fig. 4.13, of magnitude equal to \(F=47 \mathrm{~N}\). The dynamic friction coefficient between block and the inclined plane is \(\mu_{d}=0.33\). At the initial time \((t=0)\) the block is in motion along the inclined plane with velocity \(v_{i n i}=4.3 \mathrm{~m} / \mathrm{s}\) upward. It is observed that subsequently the block slows down until it stops at time \(t^{*}\).

1. Draw the forces acting on the mass \(m\) when the body is in motion;

2. Find the length of the displacement of the block up to time \(t^{*}\).

3. Calculate for \(t \geq t^{*}\) (i.e., the instant when the block stops) the magnitude and direction of the static frictional force that the plane applies on the block.

Fig. 4.13

Transcribed Image Text:

4 Forces and the Dynamics of the Particle F m V ini 90