Question: Using Euler's equation for (y(x)), prove that This equation provides an alternative method for solving problems in which the integrand (f) is not an explicit

Using Euler's equation for $y(x)$, prove that

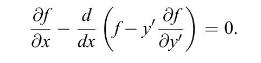
af d of = 0. dx

This equation provides an alternative method for solving problems in which the integrand $f$ is not an explicit function of $x$, because in that case the quantity $f-y^{\prime} \partial f / \partial y^{\prime}$ is constant, which is only a first-order differential equation.

af d of = 0. dx

Step by Step Solution

★★★★★

3.35 Rating (164 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Eul... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mechanics Questions!

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

Microkernel operating systems aim to address perceived modularity and reliability issues in traditional "monolithic" operating systems. (i) Describe the typical architecture of a microkernel...

CANMNMM January of this year. (a) Each item will be held in a record. Describe all the data structures that must refer to these records to implement the required functionality. Describe all the...

Question 1: (17 Marks) (i) Propose a nonlinear equation of the format f(x) = 0 that has only one non-repeated real solution. The equation must include the term (x4 + 1)-1. (ii) Give the graph of f on...

Math 1172 Project #1 Applications of Integration Due: Tuesday, September 12 Name(s): - - - - - - - - - - - - - - - - - - - - Description - - - - - - - - - - - - - - - - - - - The definite integral is...

SOLVE Questions 1-5: PLEASE AND THANK YOU 1: What is the difference between homogenous and non-homogenous differential equation? Write an example for each and solve it. 2: What is the main formula to...

Downloaded 02/28/15 to 132.174.255.3. Redistribution subject to SIAM license or copyright; see http://www.siam.org/journals/ojsa.php 15.7. Exercises 475 changes and we laugh no more. While...

A creative engineer suggests structuring the TLB so that not all the bits of the presented address need match to result in a hit. Suggest how this might be achieved, and what might be the costs and...

Math 104A Homework #3 Instructor: Lihui Chai General Instructions: Please write your homework papers neatly. You need to turn in both full printouts of your codes and the appropriate runs you made....

Section 8.5 Reading Assignment: Integration of Rational Functions by Partial Fractions Answer Only Exercise 1, 2, and 3 by using a screenshot provided Calculus Pearson textbook. Make sure you read...

In certain locales, power transmission is made by means of underground cables. In one example an 8.0-cm-diameter cable is buried at a depth of 1.3 m, and the resistance of the cable is 1.1 104 /m....

Njabulo is a 72 year old accountant at an accounting firm. He earns a taxable income of R58 470 per month and 13th cheque (bonus).He contributes 7.5% of his basic salary towards pension fund. He...

Which statement best describes how Volney B . Palmer infuenced advertiving? In 1 8 4 1 , he vet up the frst professional advertining agency in the United Stabes. In 1 8 5 9 , his advertiving apency...

5.11 Why is a payday or title loan considered predatory lending?

Determine the values of the degeneracy discriminant $\left(n \lambda^{3}ight)$ for hydrogen, helium, and oxygen at NTP. Make an estimate of the respective temperature ranges where the magnitude of...

Show that in the first approximation the partition function of a system of $N$ noninteracting, indistinguishable particles is given by \[ Q_{N}(V, T)=\frac{1}{N ! \lambda^{3 N}} Z_{N}(V, T), \]...

Study the density matrix and the partition function of a system of free particles, using the unsymmetrized wavefunction (5.4.3) instead of the symmetrized wavefunction (5.5.7). Show that, following...

which of the variables will need to be explicitly destroyed using the delete keyword

Charlie Motor Company had a balance in the allowance for doubtful accounts of $5,700 at the beginning of the year. During the year, Charlie had net credit sales of $500,000. Assuming that Charlie...

You own a portfolio invested 15 percent in Stock Q. 20% in Stock R, and 35% in Stock T. The beta for these 4 stocks are .79, 1.23, 1.13, and 1.36 respectively. What is the portfolio beta