Consider the linear regression model with scalar regressor y i = x i + u i
Question:
Consider the linear regression model with scalar regressor with data iid over though the error may be conditionally heteroskedastic.
(a) Show that .
(b) Apply Kolmogorov law of large numbers (Theorem A.8) to the averages of and to show that . State any additional assumptions made on the dgp for and .
(c) Apply the Lindeberg-Levy central limit theorem (Theorem A.14) to the averages of to show that . State any additional assumptions made on the dgp for and .
(d) Use the product limit normal rule (Theorem A.17) to show that part (c) implies . State any assumptions made on the dgp for and .
(e) Combine results using (2.14) and the product limit normal rule (Theorem A.17) to obtain the limit distribution of .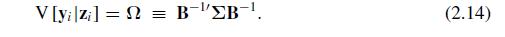

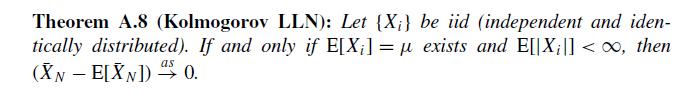
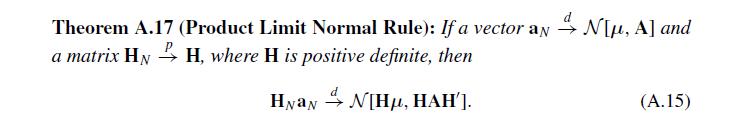
Step by Step Answer:

Microeconometrics Methods And Applications
ISBN: 9780521848053
1st Edition
Authors: A.Colin Cameron, Pravin K. Trivedi





