Consider the linear regression model y i = x i + u i with nonstochastic
Question:
Consider the linear regression model with nonstochastic regressors and error that has mean zero but is correlated as follows: if if , and if . Thus errors for immediately adjacent observations are correlated whereas errors are otherwise uncorrelated. In matrix notation we have , where uu']. For this model answer each of the following questions using results given in Section 4.4.
(a) Verify that is a band matrix with nonzero terms only on the diagonal and on the first off-diagonal; and give these nonzero terms.
(b) Obtain the asymptotic distribution of using (4.19).
(c) State how to obtain a consistent estimate of that does not depend on unknown parameters.
(d) Is the usual OLS output estimate a consistent estimate of ?
(e) Is White's heteroskedasticity robust estimate of consistent here?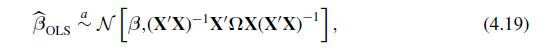




Step by Step Answer:

Microeconometrics Methods And Applications
ISBN: 9780521848053
1st Edition
Authors: A.Colin Cameron, Pravin K. Trivedi





