(a) By taking the trace of the time-dependent tensorial virial theorem and specializing to an MHD plasma with (or without) self-gravity, show that

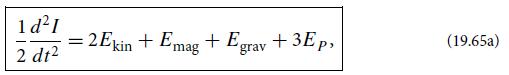
where I is the trace of I_jk, E_kin is the system’s kinetic energy, E_mag is its magnetic energy, E_P is the volume integral of its pressure, and E_grav is its gravitational self-energy:

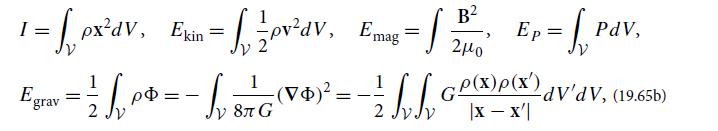
with Φ the gravitational potential energy [cf. Eq. (13.62)].
(b) When the time integral of d²I/dt² vanishes, then the time average of the righthand side of Eq. (19.65a) vanishes:

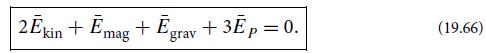
This is the time-averaged scalar virial theorem. Give examples of circumstances in which it holds.

(c) Equation (19.66) is a continuum analog of the better-known scalar virial theorem, 2E̅_kin + E̅_grav = 0, for a system consisting of particles that interact via their self-gravity—for example, the solar system.

(d) As a simple but important application of the time-averaged scalar virial theorem, show—neglecting self-gravity—that it is impossible for internal currents in a plasma to produce a magnetic field that confines the plasma to a finite volume: external currents (e.g., in solenoids) are necessary.

(e) For applications to the oscillation and stability of self-gravitating systems.

Equation 13.62.

Transcribed Image Text:

1d²1 2 dt² = = 2Ekin + Emag + Egrav +3E p, (19.65a)