(a) Show that the spatially variable part of the gravitational potential for a uniform density, nonrotating planet can be written as Φ = 2πGρr²/3, where ρ is the density.

(b) Hence argue that the gravitational potential for a slowly spinning planet can be written in the form

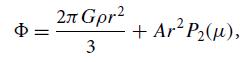
where A is a constant, and P₂ is the Legendre polynomial with argument μ = sin(latitude).What happens to the P₁ term?

(c) Give an equivalent expansion for the potential outside the planet.

(d) Now transform into a frame spinning with the planet, and add the centrifugal potential to give a total potential.

(e) By equating the potential and its gradient at the planet’s surface, show that the difference between the polar and the equatorial radii is given by

where g is the gravitational acceleration at the surface. Note that this is 5/2 times the answer for a planet whose mass is concentrated at its center [Eq. (13.28a)].

Transcribed Image Text:

2π Gpr² 3 + Ar² P₂(μ),