(a) Show that viscosity damps a monochromatic deep-water wave with an amplitude e-folding time τ_∗ = (2νk²)⁻¹, where k is the wave number, and ν is the kinematic viscosity.

(b) As an example, consider the ocean waves that one sees at an ocean beach when the surf is “up” (large-amplitude waves). These are usually generated by turbulent winds in storms in the distant ocean, 1,000 km or farther from shore. The shortest wavelengths present should be those for which the damping length Cτ_∗ is about 1,000 km; shorter wavelengths than that will have been dissipated before reaching shore. Using the turbulent viscosity ν ∼ 0.03m²s⁻¹ that we deduced from the observed thicknesses of wind-driven Ekman layers in the ocean (Ex. 14.21), compute this shortest wavelength for the large-amplitude waves, and compare with the wavelengths you have observed at an ocean beach. You should get pretty good agreement, thanks to a weak sensitivity of the wavelength to the rather uncertain turbulent viscosity.

(c) Make similar comparisons of theory and observation for,

(i) The choppy, short wavelength ocean waves that one sees when (and only when) a local wind is blowing, and 

(ii) Waves on a small lake.

Data from Exercises 14.21.

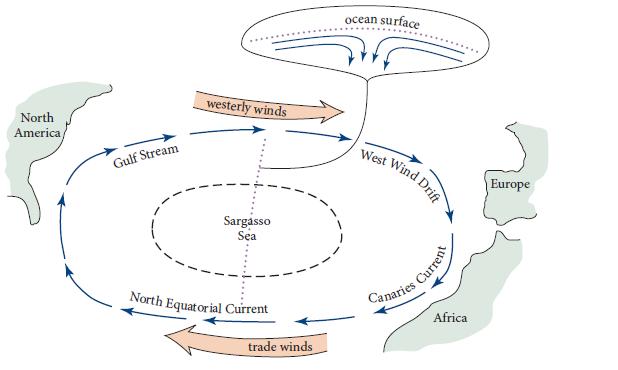
The north Atlantic Ocean exhibits the pattern of winds and ocean currents shown in Fig. 14.18. Westerly winds blow from west to east at 40° latitude. Trade winds blow from east to west at 20° latitude. In between, around 30° latitude, is the Sargasso Sea: a 1.5-m-high gyre (raised hump of water). The gyre is created by ocean surface currents, extending down to a depth of only about 30m, that flow northward from the trade-wind region and southward from the westerly wind region (upper inset in Fig. 14.18). A deep ocean current, extending from the surface down to near the bottom, circulates around the Sargasso Sea gyre in a clockwise manner. This current goes under different names in different regions of the ocean: Gulf Stream, WestWind Drift, Canaries Current, and North Equatorial Current. Explain both qualitatively and semi quantitatively (in terms of order of magnitude) how the winds are ultimately responsible for all these features of the ocean. More specifically, do the following.

(a) Explain the surface currents in terms of an Ekman layer at the top of the ocean, with thickness δ_E about 30m. From this measured δ_E compute the kinematic viscosity ν in the boundary layer. Your result, ν ∼ 0.03m² s⁻¹, is far larger than the molecular viscosity of water, ∼10⁻⁶ m² s⁻¹ (Table 13.2). The reason is that the boundary layer is turbulent, and its eddies produce this large viscosity

(b) Explain why the height of the gyre that the surface currents produce in the Sargasso Sea is about 1.5 m.

(c) Explain the deep ocean current (Gulf Stream, etc.) in terms of a geostrophic flow, and estimate the speed of this current. This current, like circulation in a tea cup, is an example of a “secondary flow.”

(d) If there were no continents on Earth, but only an ocean of uniform depth, what would be the flow pattern of this deep current—its directions of motion at various locations around Earth, and its speeds? The continents (North America, Europe, and Africa) must be responsible for the deviation of the actual current (Gulf Stream, etc.) from this continent-free flow pattern. How do you think the continents give rise to the altered flow pattern?

Table 13.2.

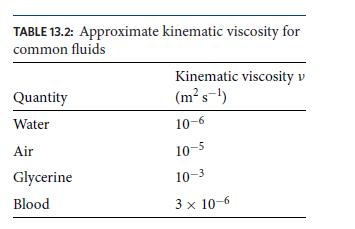
Figure 14.18.

Transcribed Image Text:

TABLE 13.2: Approximate kinematic viscosity for common fluids Quantity Water Air Glycerine Blood Kinematic viscosity v (m² s-¹) 10-6 10-5 10-3 3 x 10-6