A simplified version of a commercial nuclear reactor involves fissile material such as enriched uranium¹² and a moderator such as graphite, both of which will be assumed in this exercise. Slow (thermalized) neutrons, with kinetic energies ∼0.1 eV, are captured by the ²³⁵U nuclei and cause them to undergo fission, releasing ∼170 MeV of kinetic energy per fission which appears as heat. Some of this energy is then converted into electric power. The fission releases an average of two or three (assume two) fast neutrons with kinetic energies ∼ 1 MeV. The fast neutrons must be slowed to thermal speeds where they can be captured by ²³⁵U atoms and induce further fissions. The slowing is achieved by scattering off the moderator atoms—a scattering in which the crucial effect, energy loss, occurs in momentum space. The momentum-space scattering is elastic and isotropic in the center-of-mass frame, with total cross section (to scatter off one of the moderator’s carbon atoms) σs ≈ 4.8 × 10⁻²⁴ cm² ≡ 4.8 barns. Using the fact that in the moderator’s rest frame, the incoming neutron has a much higher kinetic energy than the moderator carbon atoms, and using energy and momentum conservation and the isotropy of the scattering, one can show that in the moderator’s rest frame, the logarithm of the neutron’s energy is reduced in each scattering by an average amount ξ that is independent of energy and is given by

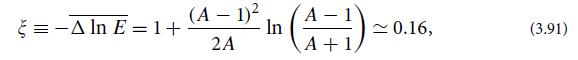
a quantity sometimes known as lethargy. Here A ≈12 is the ratio of the mass of the scattering atom to that of the scattered neutron.

There is a dangerous hurdle that the diffusing neutrons must overcome during their slowdown: as the neutrons pass through a critical energy region of about ∼7 to ∼6 eV, the ²³⁸U atoms can absorb them. The absorption cross section has a huge resonance there, with width ∼1 eV and resonance integral ∫σ_ad ln E ≈ 240 barns. For simplicity, we approximate the cross section in this absorption resonance by σ_a≈ 1600 barns at 6 eV 235U fission) to slow down through this resonant energy without getting absorbed. Those that make it through will thermalize and trigger new ²³⁵U fissions (about one per original fission), maintaining the chain reaction.

We idealize the uranium and moderator atoms as homogeneously mixed on length scales small compared to the neutron mean free path, λ_s = 1/(σ_sn_s) ≈ 2 cm, where n_s is the number density of moderator (carbon) atoms. Then the neutrons’ distribution function N, as they slow down, is isotropic in direction and independent of position; and in our steady-state situation, it is independent of time. It therefore depends only on the magnitude p of the neutron momentum or equivalently, on the neutron kinetic energy E = p²/(2m): N = N(E).

Use the Boltzmann transport equation or other considerations to develop the theory of the slowing of the neutrons in momentum space and of their struggle to pass through the ²³⁸U resonance region without getting absorbed. More specifically, do the following.

(a) Use as the distribution function not N(E) but rather n_E(E) ≡ dN/dV_xdE = (number of neutrons per unit volume and per unit kinetic energy), and denote by q(E) the number of neutrons per unit volume that slow down through energy E per unit time. Show that outside the resonant absorption region these two quantities are related by

is the neutron speed, so q contains the same information as the distribution function n_E. Explain why the steady-state operation of the nuclear reactor requires q to be independent of energy in this nonabsorption region, and infer that n_E ∝ E^−3/2.(b) Show further that inside the resonant absorption region, 6 eV

Here n_s is the number density of scattering (carbon) atoms, and n_a is the number density of absorbing (²³⁸U) atoms. Then show that the absorption causes q to vary with energy according to the following differential equation:

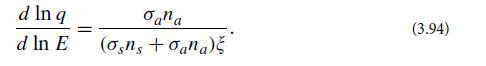
(c) By solving this differential equation in our idealization of constant σ_a over the range 7 to 6 eV, show that the condition to maintain the chain reaction is

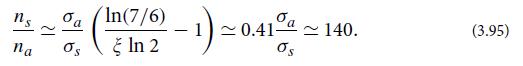
Thus, to maintain the reaction in the presence of the huge ²³⁸U absorption resonance for neutrons, it is necessary that approximately 99% of the reactor volume be taken up by moderator atoms and 1% by uranium atoms.

Transcribed Image Text:

-A ln E = 1+ (A − 1)² 2A ¹ ( ₁ + ¹) = +1 In ≈ 0.16, (3.91)