(a) Use the Helmholtz-Kirchhoff integral (8.4) or (8.6) to compute all four pieces of the holographically reconstructed wave field. Show that the piece generated by

is the same (aside from overall amplitude) as the field

that would have resulted if when making the hologram (Fig. 10.6), the mirror wave had been absent and the photographic plate replaced by a window. Show that the other pieces have the forms and propagation directions indicated heuristically in Fig. 10.8. We shall examine the secondary wave, generated by

in Ex. 10.6.

(b) Suppose that plane-parallel white light is used in the holographic reconstruction of Fig. 10.8. Derive an expression for the direction in which one sees the object’s 3-dimensional image have a given color (or equivalently, wave number). Assume that the original hologram was made with green light and θ_o = 45◦. What are the angles at which one sees the image as violet, green, yellow, and red?

Data from Exercises 10.6

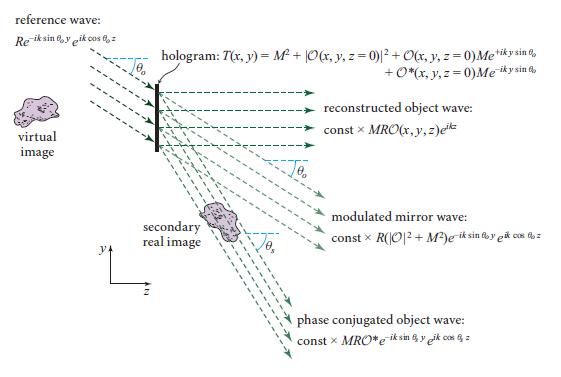
Consider the secondary wave generated by

the holographic reconstruction process of Fig. 10.8, Eq. (10.7), and Ex. 10.2.

(a) Assume, for simplicity, that the mirror and reference waves propagate nearly perpendicular to the hologram, so θo « 90◦ and θ_s ≈ 2θo « 90◦; but assume that θ_s is still large enough that fairly far from the hologram the object wave and secondary waves separate cleanly from each other. Then, taking account of the fact that the object wave field has the form O(x, y, z)e^ikz, show that the secondary wave is the phase-conjugated object wave defined in this section, except that it is propagating in the +z direction rather than −z (i.e., it has been reflected through the z = 0 plane). Then use this and the discussion of phase conjugation in the text to show that the secondary wave carries an image that resides in front of the hologram and is turned inside out, as discussed near the end of Sec. 10.3. Show, further, that if θo is not90◦ (but is s is a real angle, and the secondary image actually exists), then the secondary image is changed by a distortion along the y direction. What is the nature of the distortion, a squashing or a stretch?

(b) Suppose that a hologram has been made with θ_o

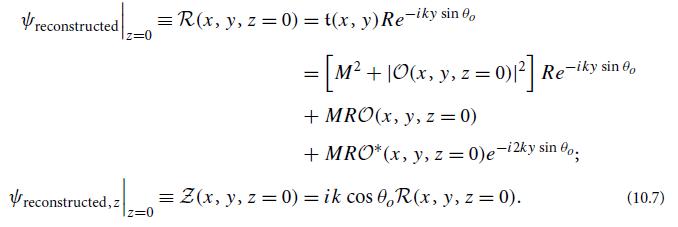
Figure 10.6

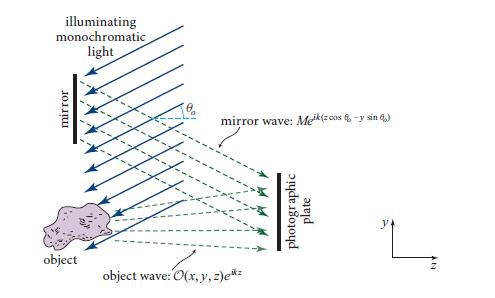
Figure 10.8.

tx O(x, y, z = 0) Meiky sin o