Burkes radiation-reaction potential (27.64) produces a force per unit volume react on its nearly Newtonian source.
Question:
Burke’s radiation-reaction potential (27.64) produces a force per unit volume −ρ∇Φreact on its nearly Newtonian source. If we multiply this force per unit volume by the velocity v = dx/dt of the source’s material, we obtain thereby a rate of change of energy per unit volume. Correspondingly, the net rate of change of the system’s mass-energy must be
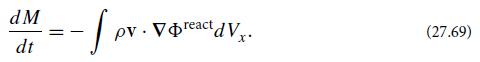
Show that, when averaged over a few gravitational-wave periods, this formula agrees with the rate of change of mass (27.61) that we derived in Ex. 27.11 by integrating the outgoing waves’ energy flux.
Data from Exercises 27.11.
(a) Compute the net rate at which the quadrupolar waves (27.57) carry energy away from their source, by carrying out the surface integral (25.102) with T0j being Isaacson’s gravitational-wave energy flux (27.40). Your answer should be Eq. (27.61).
(b) The computation of the waves’ angular momentum can be carried out in the same way, but is somewhat delicate, because a tiny non-radial component of the energy flux, that dies out as 1/r3, gives rise to the O(1/r2) angular momentum flux
Equations.

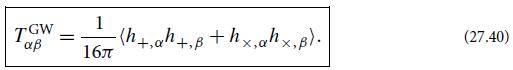

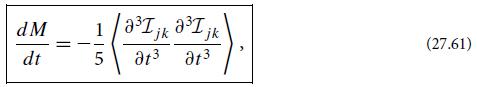

Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





