Canonical transformations are treated in advanced textbooks on mechanics, such as Goldstein, Poole, and Safko or, more concisely, Landau and Lifshitz (1976). This exercise gives a brief introduction. For simplicity we assume the hamiltionian is time independent.

Let (q_j , p_k) be one set of generalized coordinates and momenta for a given system. We can transform to another set (Q_j , P_k), which may be more convenient, using a generating function that connects the old and new sets. One type of generating function is F(q_j , P_k), which depends on the old coordinates {q_j} and new momenta {P_k}, such that

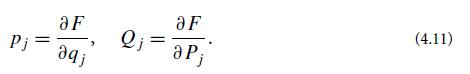
(a) As an example, what are the new coordinates and momenta in terms of the old that result from

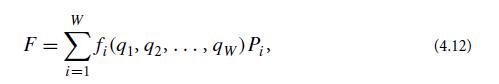
where fi are arbitrary functions of the old coordinates?

(b) The canonical transformation generated by Eq. (4.11) for arbitrary F(q_j , P_k) leaves unchanged the value, but not the functional form, of the hamiltonian at each point in phase space. In other words, H is a geometric, coordinate independent function (scalar field) of location in phase space. Show, for the special case of a system with one degree of freedom (one q, one p, one Q, and one P), that if Hamilton’s equations (4.1) are satisfied in the old variables (q , p), then they will be satisfied in the new variables (Q, P).

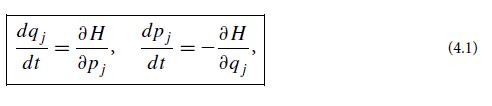
(c) Show, for a system with one degree of freedom, that although dq ≠ dQ and dp ≠ dP, the volume in phase space is unaffected by the canonical transformation: dpdq = dPdQ.

(d) Hence show that for any closed path in phase space,

These results are readily generalized to more than one degree of freedom.

Pj a F 2qj Qj= a F a Pi (4.11)