Compute the velocity profile of a conducting fluid in a duct of thickness 2a perpendicular to externally generated, uniform electric and magnetic fields (E₀e_y and B₀e_z) as shown in Fig. 19.7. Away from the vertical sides of the duct, the velocity v_x is just a function of y, and the pressure can be written in the form P = −Qx + p(z), where Q is the longitudinal pressure gradient.

(a) Show that the velocity field satisfies the differential equation

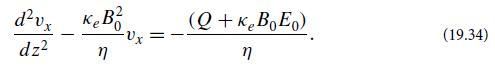
(b) Impose suitable boundary conditions at the bottom and top walls of the channel, and solve this differential equation to obtain the following velocity field:

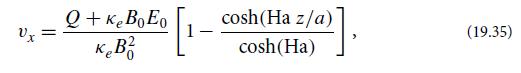
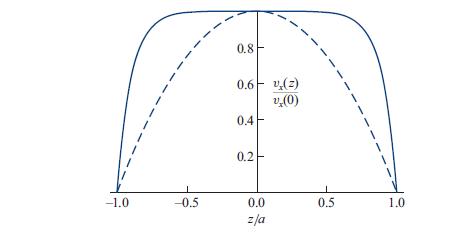
where Ha is the Hartmann number (see Fig. 19.9).

Fig. 19.7.

Figure 19.9. 

Transcribed Image Text:

d²vx dz² - Ke B² Vx 17 (Q+K₂B₂Eo) n (19.34)