Consider a 1-dimensionalwave packet with dispersion relation = (k). For concreteness, let A(k)be a narrow Gaussian
Question:
Consider a 1-dimensionalwave packet
![]()
with dispersion relation ω = Ω(k). For concreteness, let A(k)be a narrow Gaussian peaked around
![]()
(a) Expand α as α(k) = αo − xoκ with xo a constant, and assume for simplicity that higher order terms are negligible. Similarly, expand ω ≡ Ω(k) to quadratic order and explain why the coefficients are related to the group velocity Vg at k = ko by Ω = ωo + Vgκ + (dVg/dk)κ2/2.
(b) Show that the wave packet is given by
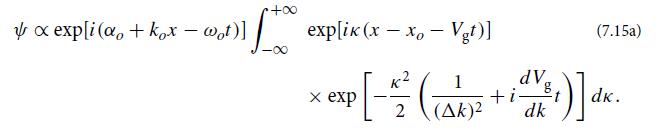 (c) Evaluate the integral analytically. From your answer, show that the modulus of ψ satisfies
(c) Evaluate the integral analytically. From your answer, show that the modulus of ψ satisfies
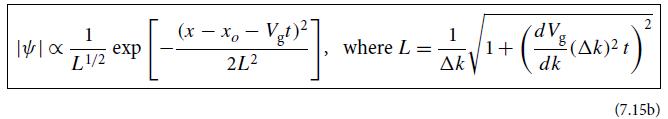
is the packet’s half-width.
(d) Discuss the relationship of this result at time t = 0 to the uncertainty principle for the localization of the packet’s quanta.
(e) Equation (7.15b) shows that the wave packet spreads (i.e., disperses) due to its containing a range of group velocities [Eq. (7.11)]. How long does it take for the packet to enlarge by a factor 2? For what range of initial half-widths can a water wave on the ocean spread by less than a factor 2 while traveling from Hawaii to California?
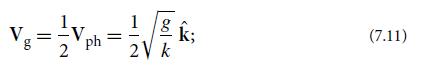
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





