Consider a microcanonical ensemble of closed cubical cells with volume V . Let each cell contain precisely
Question:
Consider a microcanonical ensemble of closed cubical cells with volume V . Let each cell contain precisely N particles of a classical, nonrelativistic, perfect gas and contain a nonrelativistic total energy
![]()
For the moment (by contrast with the text’s discussion of the microcanonical ensemble), assume that E is precisely fixed instead of being spread over some tiny but finite range.(a) Explain why the region Yo of phase space accessible to each system is
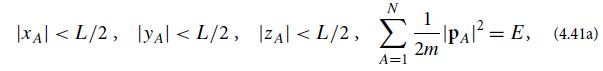
where A labels the particles, and L ≡ V1/3 is the side of the cell.(b) To compute the entropy of the microcanonical ensemble, we compute the volume![]() in phase space that it occupies, multiply by the number density of states in phase space (which is independent of location in phase space), and then take the logarithm. Explain why.
in phase space that it occupies, multiply by the number density of states in phase space (which is independent of location in phase space), and then take the logarithm. Explain why.
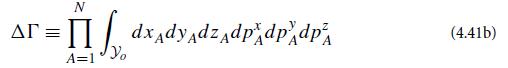
vanishes. This illustrates the “set of measure zero” statement in the text, which we used to assert that we must allow the systems’ energies to be spread over some tiny but finite range.(c) Now permit the energies of our ensemble’s cells to lie in the tiny but finite range Eo − δEo
![]()
where Vν(a) is the volume of a sphere of radius a in a Euclidean space with ν >> 1 dimensions, and where
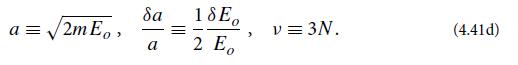
It can be shown (and you might want to try to show it) that
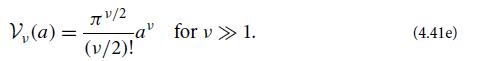
(d) Show that, so long as 1 >> δEo/Eo >> 1/N (where N in practice is an exceedingly huge number),
![]()
which is independent of δEo and thus will produce a value for![]() and thence Nstates and S independent of δEo, as desired. From this and with the aid of Stirling’s approximation (Reif, 2008, Appendix A.6) n! ≈ (2πn)1/2(n/e)n for large n, and taking account of the multiplicity M = N!, show that the entropy of the microcanonically distributed cells is given by
and thence Nstates and S independent of δEo, as desired. From this and with the aid of Stirling’s approximation (Reif, 2008, Appendix A.6) n! ≈ (2πn)1/2(n/e)n for large n, and taking account of the multiplicity M = N!, show that the entropy of the microcanonically distributed cells is given by
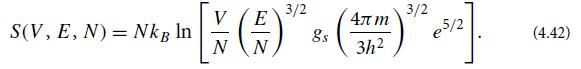
This is known as the Sackur-Tetrode equation.
(e) Using Eqs. (3.39), show that this is equivalent to Eq. (4.40) for the entropy, which we derived by a very different method.

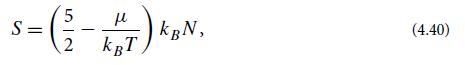
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





