Consider a sound wave propagating through a static, inhomogeneous fluid with no gravity. Explain why the unperturbed
Question:
Consider a sound wave propagating through a static, inhomogeneous fluid with no gravity. Explain why the unperturbed fluid has velocity v = 0 and pressure Po = constant, but can have variable density and sound speed, ρo(x) and C(x, t). By repeating the analysis in Eqs. (16.47)–(16.50), show that the wave equation is ∂2δP/∂t2 = C2ρo ∇· (ρo−1∇δP), which can be rewritten as

where W = (C2ρo)−1.
Equation (16.54) is an example of the prototypical wave equation (7.17) that we used in Sec. 7.3.1 to illustrate the geometric-optics formalism. The functional form of W and the placement of W and C2 (inside versus outside the derivatives) have no influence on the wave’s dispersion relation or its rays or phase in the geometric-optics limit, but they do influence the propagation of the wave’s amplitude. See Sec. 7.3.1.
Equations
![]()



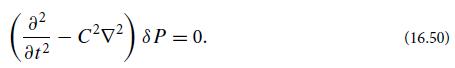

Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





