Consider a wave propagating through a dielectric medium that is anisotropic, but not necessarily—for the moment—axisymmetric. Let the wave be sufficiently weak that nonlinear effects are unimportant. Then the nonlinear wave equation (10.22a) takes the linear form

(a) Specialize to a monochromatic plane wave with angular frequency ω and wave vector k. Show that the wave equation (10.50) reduces to

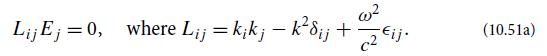
This equation says that E_j is an eigenvector of L_ij with vanishing eigenvalue, which is possible if and only if

(b) Next specialize to an axisymmetric medium, and orient the symmetry axis along the z direction, so the only nonvanishing components of the dielectric tensor ∈_ij are ∈₁₁ = ∈₂₂ and ∈₃₃. Let the wave propagate in a direction K̂ that makes an angle θ to the symmetry axis. Show that in this case L_ij has the form

and the dispersion relation (10.51b) reduces to

where

in accord with Eq. (10.39).

(c) Show that this dispersion relation has the two solutions (ordinary and extraordinary) discussed in the text, Eqs. (10.40a) and (10.40b), and show that the electric fields associated with these two solutions point in the directions described in the text.

Equations.

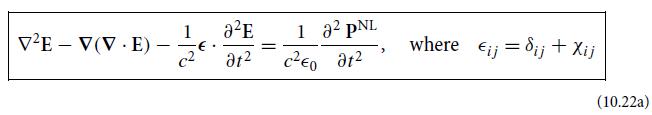
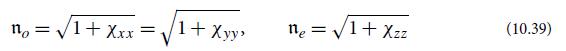
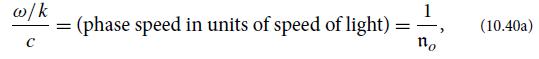
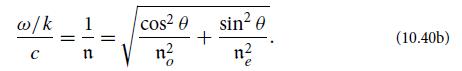
-VE+ V(VE) = - aE . a (10.50)