Consider an ideal gas consisting of several different particle species (e.g., diatomic oxygen molecules and nitrogen molecules

Question:

Consider an ideal gas consisting of several different particle species (e.g., diatomic oxygen molecules and nitrogen molecules in the case of Earth’s atmosphere).Consider a sample of this gas with volume V, containing N_A particles of various species A, all in thermodynamic equilibrium at a temperature T sufficiently low that we can ignore the effects of special relativity. Let species A have ν_A internal degrees of freedom with the hamiltonian quadratic in their generalized coordinates (e.g., rotation and vibration), and assume that those degrees of freedom are sufficiently thermally excited to have reached energy equipartition. Then the equipartition theorem dictates that each such particle has 3/2k_BT of translational energy plus 1/2ν_Ak_BT of internal energy, and because the gas is ideal, each particle contributes k_BT/V to the pressure. Correspondingly, the sample’s total energy E and pressure P are

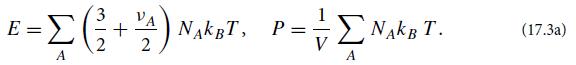
(a) Use the laws of thermodynamics to show that the specific heats at fixed volume and pressure are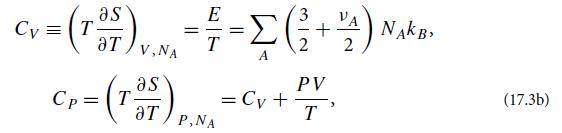

(b) If there are no thermalized internal degrees of freedom, νA = 0 (e.g., for a fully ionized, nonrelativistic gas), then γ = 5/3. For Earth’s atmosphere, at temperatures between about 10 K and 400 K, the rotational degrees of freedom of the O₂ and N₂ molecules are thermally excited, but the temperature is too low to excite their vibrational degrees of freedom. Explain why this means that ν_O2 = ν_N2 = 2, which implies γ = 7/5 = 1.4.

(c) Between about 1,300 K and roughly 10,000 K the vibrational degrees of freedom are thermalized, but the molecules have not dissociated substantially into individual atoms, nor have they become substantially ionized. Explain why this means that ν_O2 = ν_N2 = 4 in this temperature range, which implies γ = 9/7 ≈ 1.29.

(d) At roughly 10,000 K the two oxygen atoms in O₂ dissociate, the two nitrogen atoms in N₂ dissociate, and electrons begin to ionize. Explain why this drives γ up toward 5/3 ≈ 1.67.

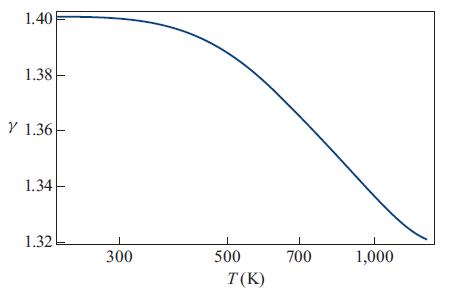
The actual value of γ as a function of temperature for the range 200 K to 1,300 K is shown in Fig. 17.3. Evidently, as stated, γ = 1.4 is a good approximation only up to about 400 K, and the transition toward γ = 1.29 occurs gradually between about 400 K and 1,400 K as the vibrational degrees of freedom gradually become thermalized and begin to obey the equipartition theorem.

Figure 17.3.