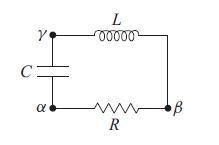
Question: Consider an L-C-R circuit as shown in Fig. 6.15. This circuit is governed by the differential equation (6.72), where F is the fluctuating voltage produced
Consider an L-C-R circuit as shown in Fig. 6.15. This circuit is governed by the differential equation (6.72), where F´ is the fluctuating voltage produced by the resistor’s microscopic degrees of freedom (so we shall rename it V´), and F ≡ V vanishes, since there is no driving voltage in the circuit. Assume that the resistor has temperature T >> ℏωo/k, where ωo = (LC)−1/2 is the circuit’s resonant angular frequency, ωo = 2πfo, and also assume that the circuit has a large quality factor (weak damping) so R ≪ 1/(ωoC) ≈ ωoL.
(a) Initially consider the resistor R decoupled from the rest of the circuit, so current cannot flow across it. What is the spectral density Vαβ of the voltage across this resistor?
(b) Now place the resistor into the circuit as shown in Fig. 6.15. The fluctuating voltage V´ will produce a fluctuating current I = q̇ in the circuit (where q is the charge on the capacitor).What is the spectral density of I? And what, now, is the spectral density Vαβ across the resistor?
(c) What is the spectral density of the voltage Vαγ between points α and γ? and of Vβγ ?
(d) The voltage Vαβ is averaged from time t = t0 to t = t0 + τ (with τ >> 1/fo), giving some average value U0. The average is measured once again from t1 to t1 + τ , giving U1. A long sequence of such measurements gives an ensemble of numbers {U0, U1, . . . , Un}. What are the mean U̅ and rms deviation △U ≡ ((U − U̅)2)1/2 of this ensemble?
Equation 6.72
![]()
Fig 6.15
L+Cq = Fbath (t) = R + F', (6.72)
Step by Step Solution
3.53 Rating (160 Votes )
There are 3 Steps involved in it
a Since the resistor is initially decoupled from the rest of the circuit there is no current flowing through it and hence no voltage drop across it Th... View full answer

Get step-by-step solutions from verified subject matter experts


