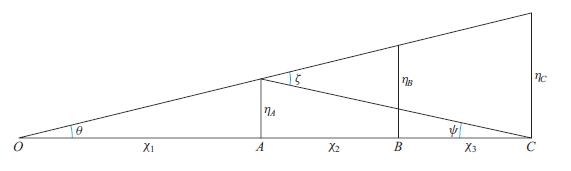
Consider the triangle formed by the three geodesics in Fig. 28.3. In a flat space, the exterior angle must equal + . However,

Consider the triangle formed by the three geodesics in Fig. 28.3. In a flat space, the exterior angle ζ must equal θ + ψ. However, if the space is homogeneous and positively curved, then the angle deficit △ ≡ θ + ψ − ζ will be positive.

(a) By considering the geometry of the 2-dimensional surface of a sphere embedded in 3-dimensional Euclidean space, show that the area of the triangle is △/K.

(b) Make a conjecture (or, better still, devise a demonstration) as to the formula for the area of a triangle in a negatively curved homogeneous space.

These results are special cases of the famous Gauss-Bonnet theorem, which allows for the possibility that the topology of the space might not be simple.

Figure 28.3.

0 X1 MA A X MB B X3 nc