Cosmic ray particles with energies between ∼1GeV and ∼1PeV are believed to be accelerated at the strong shock fronts formed by supernova explosions in the strongly scattering, local, interstellar medium. We explore a simple model of the way in which this happens.

(a) In a reference frame where the shock is at rest, consider the stationary (time independent) flow of a medium (a plasma) with velocity u(x) e_x, and consider relativistic cosmic rays, diffusing through the medium, that have reached a stationary state. Assume that the mean free paths of the cosmic rays are so short that their distribution function f = dN/dV_xdV_p is nearly isotropic in the local rest frame of the medium, so f = f₀(p̃, x) + f₁(p, x), where p̃ is the magnitude of a cosmic ray’s momentum as measured in the medium’s local rest frame, p̃ ≡ |p̃|, f₀ ≡ (f)  is the average over cosmic-ray propagation direction in the medium’s local rest frame, and |f₁| ≪ |f₀|. Show that in terms of the cosmic ray’s momentum p = |p| and energy

as measured in the shock’s rest frame, p̃ = p − u(x)ε cos θ, where θ is the angle between p and the direction e_x of the
medium’s motion.

(b) By expanding the full Vlasov equation to second order in the ratio of the scattering mean free path to the scale on which u(x) varies, it can be shown (e.g., Blandford and Eichler, 1987, Sec. 3.5) that, in the shock’s frame,

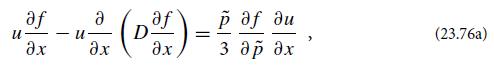
where D(p̃ , x) > 0 is the spatial diffusion coefficient which arises from f₁. Explore this convection-diffusion equation. For example, by integrating it over momentum space in the shock’s frame, show that it conserves cosmic ray particles. Also, show that, when the diffusion term is unimportant, f₀ is conserved moving with the medium’s flow in the sense that u∂f0/∂x + (dp̃/dt)∂f₀/∂p̃ = 0, where dp̃/dt is the rate of change of cosmic ray momenta due to elastic scattering in the expanding medium (for which a volume element changes as d ln V_x/dt = ∂u/∂x).

(c) Argue that the flux of cosmic-ray particles, measured in the shock’s frame, is given by ∫₀^∞(p, x)4πp²dp, where F(p, x) = −D(∂f₀/∂x) − u(p/3)(∂f/∂p̃); or, to leading order in u/v, where v = p/ε is the cosmic ray speed,

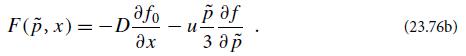
This F is often called the flux of particles at momentum p̃ .

(d) Idealize the shock as a planar discontinuity at x = 0 in the medium’s velocity u(x); idealize the velocity as constant before and after the shock, u = u₋ = constant for x + = constant for x > 0; and denote by r = u₋/u₊ > 1 the shock’s compression ratio. Show that upstream from the shock, the solution to the convection-diffusion equation (23.76a) is

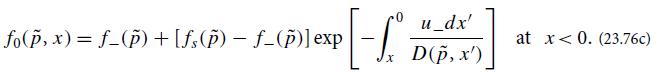
Here f−(p̃) ≡ f₀(p̃, x = −∞), and fs(p̃) ≡ f₀(p̃ , x = 0) is the value of f₀ at the shock, which must be continuous across the shock. (Why?) Show further that downstream from the shock f₀ cannot depend on x, so

(e) By matching the flux of particles at momentum p̃, F(p̃ , x) [Eq. (23.76b)], across the shock, show that the post-shock distribution function is

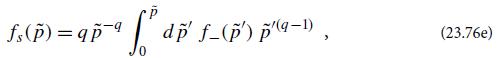
where q = 3r/(r − 1).

(f) The fact that this stationary solution to the convection-diffusion equation has a power-law spectrum f_s ∝ p̃^−q, in accord with observations, suggests that the observed cosmic rays may indeed be accelerated in shock fronts. How, physically, do you think the acceleration occurs and how does this lead to a power-law spectrum? What is the energy source for the acceleration? It may help to explore the manner in which Eq. (23.76c) evolves an arbitrary initial distribution function f−(p̃) into the power-law distribution (23.76d).

Transcribed Image Text:

E = √√√p² + m²