Here is an example of how to use index notation to derive a vector identity for the
Question:
Here is an example of how to use index notation to derive a vector identity for the double cross product A × (B × C): in index notation this quantity is ∈ij kAj (∈klmBlCm). By permuting the indices on the second ∈ and then invoking Eq. (1.23), we can write this as
![]()
By then invoking the meaning of the 4-index delta function [Eq. (1.23)], we bring this into the form AjBiCj − AjBjCi, which is the slot-naming index-notation form of (A · C)B − (A · B)C. Thus, it must be that A × (B × C) = (A · C)B− (A · B)C. Use similar techniques to evaluate the following quantities.(a) ∇ × (∇ × A).(b) (A × B) · (C × D).(c) (A × B) × (C × D).
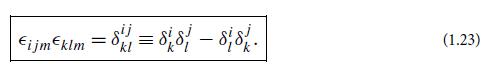
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford
Question Posted:





