In any high-precision Foucault pendulum, it is important that the pendular restoring force be isotropic, since anisotropy will make the swinging period different in different planes and thereby cause precession of the plane of swing.

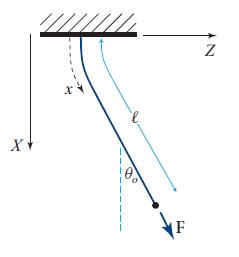
(a) Consider a pendulum of mass m and length ℓ suspended (as shown in Fig. 11.9) by a rectangular wire with thickness h in the plane of the bend (X-Z plane) and thickness w orthogonal to that plane (Y direction). Explain why the force that the wire exerts on the mass is approximately

where g is the acceleration of gravity, θ_o is defined in the figure, and θ̇_o is the time derivative of θ_o due to the swinging of the pendulum. In the second term we have assumed that the wire is long compared to its region of bend. Express the second term in terms of the amplitude of swing θ_o^max, and show that for small amplitudes

Use this approximation in the subsequent parts.

(b) Assuming that all along the wire, its angle θ(x) to the vertical is small, θ «1, show that

where λ (not to be confused with the second Lamé coefficient) is

∈ = ξx, x is the longitudinal strain in the wire, and h is the wire’s thickness in the plane of its bend.

(c) Hence show that the shape of the wire is given in terms of Cartesian coordinates by

to leading order in λ, and that the pendulum period is

(d) Finally, show that the pendulum periods when swinging along e_x and e_y differ by

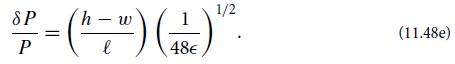
From Eq. (11.48e) one can determine how accurately the two thicknesses h and w must be equal to achieve a desired degree of isotropy in the period. A similar analysis can be carried out for the more realistic case of a slightly elliptical wire.

Figure 11.9.

-F = -(mg cos 0 + ml0)ex,