In this exercise we illustrate linearized theory by computing the gravitational field of a moving particle with
Question:
In this exercise we illustrate linearized theory by computing the gravitational field of a moving particle with finite rest mass and then that of a zero-rest-mass particle that moves with the speed of light.
(a) From Eq. (25.91), deduce that, for a particle with mass M at rest at the origin, the only nonvanishing component of h̅μν is h̅00 = 4M/r.
(b) Regarding h̅μν as a field that lives in flat spacetime, show that it can be written in frame-independent, special relativistic form as

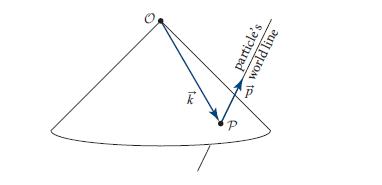
where p(vector) is the particle’s 4-momentum, and k(vector) is the past-directed null vector that reaches from the observation event O to the event P at which the particle’s world line passes through the observer’s past light cone; see Fig. 25.4. Equation (25.92) is a very powerful formula. It is an explicit form of the solution (25.91) to the wave equation (25.90) not only for a particle that moves inertially (and thus could be at rest in our original reference frame) but also for an arbitrarily accelerated particle. Explain why.
(c) In the Lorentz rest frame of the observer, let the particle move along the xaxis with speed v, so its world line is {x = vt, y = z = 0}, and its 4-momentum has components
![]()
Show, further, that the linearized spacetime metric is
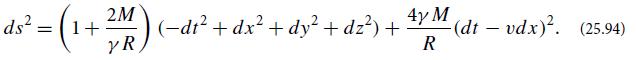
(d) Take the limit of a zero-rest-mass particle moving at the speed of light by sending m → 0, v → 1, and Mγ → ε (the particle’s energy). [The limit of
![]()
is quite tricky. It turns out to be 1/|x − t| − δ(x − t) ln(y2 + z2), where δ is the Dirac delta function (Aichelberg and Sexl, 1971).] Show that the resulting metric is
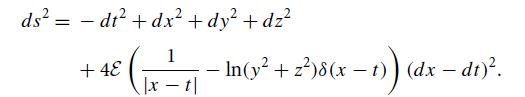
By a change of coordinates, get rid of the 1/|x − t | term, thereby obtaining our final form for the metric of a zero-rest-mass particle:
![]()
Equation (25.95) turns out to be an exact solution of the fully nonlinear Einstein field equation for a zero-rest-mass particle; it is called the Aichelberg-Sexl ultra boost solution. Just as, when a charged particle is accelerated to near light speed, its electric field lines are compressed into its transverse plane, so the metric (25.95) has all its deviations from flat spacetime concentrated in the particle’s transverse plane.
Equations.

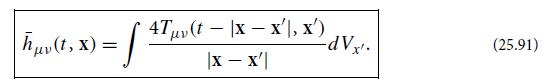
Figure 25.4.
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





