Jeans’ theorem is of great use in studying the motion of stars in a galaxy. The stars are also almost collisionless and can be described by a distribution function f(v, x, t). However, there is only one sign of “charge” and no possibility of screening. In this problem, we make a model of a spherical galaxy composed of identical-mass stars.

(a) The simplest type of distribution function is a function of one integral of a star’s motion, the energy per unit mass: E = 1/2v² + Φ, where Φ is the gravitational potential. A simple example is f (E) ∝ | − E|^7/2 for negative energy and zero for positive energy. Verify that the associated mass density satisfies: ρ ∝ [1+ (r/s)²]^−5/2, where r is the radius, and s is a scale that you should identify.

(b) This density profile does not agree with observations, so we need to find an algorithm for computing the distribution function that gives a specified density profile. Show that for a general f(E) satisfying appropriate boundary conditions,

where m is the mass of a star.

(c) Equation (22.15a) is an Abel integral equation. Confirm that it can be inverted to give the desired algorithm:

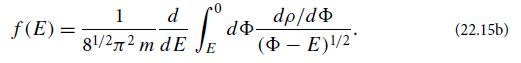
(d) Compute the distribution function that is paired with the Jaffe profile, which looks more like a real galaxy:

(e) We can construct two-integral spherical models using f (E, L), where L is a star’s total angular momentum per unit mass. What extra feature can we hope to capture using this broader class of distribution functions?

Transcribed Image Text:

dp do -8¹/2π mf d It m dE ƒ(E) (E-)1/2¹ (22.15a)