Place tea leaves and water in a tea cup, glass, or other larger container. Stir the water

Question:

Place tea leaves and water in a tea cup, glass, or other larger container. Stir the water until it is rotating uniformly, and then stand back and watch the motion of the water and leaves. Notice that the tea leaves tend to pile up at the cup’s center. An Ekman boundary layer on the bottom of the cup is responsible for this phenomenon. In this exercise you explore the origin and consequences of this Ekman layer.

(a) Evaluate the pressure distribution P(ω̅, z) in the bulk flow (outside all boundary layers), assuming that it rotates rigidly. (Here z is height and ω̅ is distance from the water’s rotation axis.) Perform your evaluation in the water’s rotating reference frame. From this P(ω̅, z) deduce the shape of the top surface of the water. Compare your deduced shape with the actual shape in your experiment.

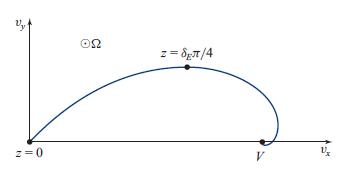
(b) Estimate the thickness of the Ekman layer at the bottom of your container. It is very thin. Show, using the Ekman spiral diagram (Fig. 14.17), that the water in this Ekman layer flows inward toward the container’s center, causing the tea leaves to pile up at the center. Estimate the radial speed of this Ekman-layer flow and the mass flux that it carries.

(c) To get a simple physical understanding of this inward flow, examine the radial gradient ∂P/∂ω̅ of the pressure P in the bulk flow just above the Ekman layer. Explain why ∂P/∂ω̅ in the Ekman layer will be the same as in the rigidly rotating flow above it. Then apply force balance in an inertial frame to deduce that the water in the Ekman layer will be accelerated inward toward the center.

(d) Using geostrophic-flow arguments, deduce the fate of the boundary-layer water after it reaches the center of the container’s bottom. Where does it go? What is the large-scale circulation pattern that results from the “driving force” of the Ekman layer’s mass flux? What is the Ross by number for this large-scale circulation pattern? How and where does water from the bulk, nearly rigidly rotating flow, enter the bottom boundary layer so as to be swept inward toward the center?

(e) Explain how this large-scale circulation pattern can mix much of the water through the boundary layer in the time t_E of Eq. (14.70). What is the value of this t_E for the water in your container? Explain why this, then, must also be the time for the angular velocity of the bulk flow to slow substantially. Compare your computed value of t_E with the observed slow-down time for the water in your container.

Equation 14.70.