We explore the structure of the wake behind the cylinder when the Reynolds number is high enough that the flow is turbulent. For comparison, here we compute the wake’s structure at lower Reynolds numbers, when the wake is laminar.

This computation is instructive: using order-of-magnitude estimates first, followed by detailed calculations, it illustrates the power of momentum conservation. It is our first encounter with the velocity field in a wake.

(a) Begin with an order-of-magnitude estimate. Characterize the wake by its width w(x) at distance x downstream from the cylinder and by the reduction in the flow velocity (the “velocity deficit”), u_o(x) ≡ V − v_x(x), at the center of the wake; see Fig. 15.3. From the diffusion of vorticity show that

Figure 15.3.

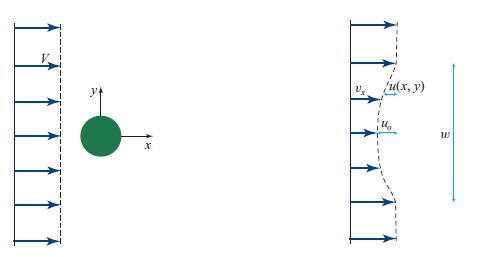
(b) Explain why momentum conservation requires that the force per unit length on the cylinder, F_D = C_D 1/2ρV²d [Eq. (15.5)], equals the transverse integral ∫T_xxdy of the fluid’s kinetic stress (T_xx = ρv_xv_x) before the fluid reaches the sphere, minus that integral at distance x after the sphere. Use this requirement to show that the fractional velocity deficit at the center of the wake is

Equation. 15.5.

(c) For a more accurate description of the flow, solve the Navier-Stokes equation to obtain the profile of the velocity deficit, u(x, y) ≡ V − v_x(x, y). Your answer should be

where w and u_o are more accurate values of the wake’s width and its central velocity deficit.

w ~2vx/V.