When analyzing the stability of configurations for magnetic confinement of a plasma (Sec. 19.5), one needs boundary
Question:
When analyzing the stability of configurations for magnetic confinement of a plasma (Sec. 19.5), one needs boundary conditions at the plasma-vacuum interface for the special case of perfect MHD (electrical conductivity idealized as arbitrarily large).
Denote by a tilde (B̃ and Ẽ) the magnetic and electric fields in the vacuum, and reserve non-tilde symbols for quantities on the plasma side of the interface.
(a) Show that the normal-force boundary condition (19.19f) reduces to an equation for the vacuum region’s tangential magnetic field:

(b) By combining Eqs. (19.19c) and (19.19g) and noting that vn − vsn must vanish (why?), and assuming that the magnetic confinement entails surface currents on the interface, show that the normal component of the magnetic field must vanish on both sides of the interface:
![]()
(c) When analyzing energy flow across the interface, it is necessary to know the tangential electric field. On the plasma side Ẽt is a secondary quantity fixed by projecting tangentially the relation E + v × B = 0. On the vacuum side it is fixed by the boundary condition (19.19e). By combining these two relations, show that
![]()
Equation 19.19(e) and 19.19(f)
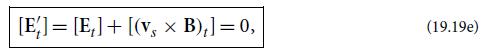
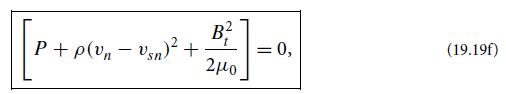
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





