When dealing with differential equations describing a physical system, it is often helpful to convert to dimensionless
Question:
When dealing with differential equations describing a physical system, it is often helpful to convert to dimensionless variables. Polytropes (nonrotating, spherical fluid bodies with the polytropic equation of state P = Kρ1+1) are a nice example.
(a) Combine the two equations of stellar structure (13.16) to obtain a single second order differential equation for P and ρ as functions of r.
(b) In the equation frompart (a) setP = Kρ1+1 to obtain a nonlinear, second-order differential equation for ρ(r).
(c) It is helpful to change dependent variables from ρ(r) to some other variable, call it θ(r), so chosen that the quantity being differentiated is linear in θ and the only θ nonlinearity is in the driving term. Show that choosing ρ ∝ θn achieves this.
(d) It is helpful to choose the proportionality constant in ρ ∝ θn in such a way that θ is dimensionless and takes the value 1 at the polytrope’s center and 0 at its surface. This is achieved by setting
![]()
where ρc is the polytrope’s (possibly unknown) central density.
(e) Similarly, it is helpful to make the independent variable r dimensionless by setting r = aξ, where a is a constant with dimensions of length. The value of a should be chosen wisely, so as to simplify the differential equation as much as possible. Show that the choice

brings the differential equation into the form

Equation (13.22) is called the Lane-Emden equation of stellar structure, after Jonathan Homer Lane and Jacob Robert Emden, who introduced and explored it near the end of the nineteenth century. There is an extensive literature on solutions of the Lane-Emden equation (see, e.g., Chandrasekhar, 1939, Chap. 4; Shapiro and Teukolsky, 1983, Sec. 3.3).
(f) Explain why the Lane-Emden equation (13.22) must be solved subject to the following boundary conditions (where θ' ≡ dθ/dξ):
![]()
(g) One can integrate the Lane-Emden equation, numerically or analytically, outward from ξ = 0 until some radius ξ1 at which θ (and thus also ρ and P) goes to zero. That is the polytrope’s surface. Its physical radius is then R = aξ1, and its mass is M =∫0R 4πρr2dr, which is readily shown to be
![]()
Then, using the value of a given in Eq. (13.21b), we have:
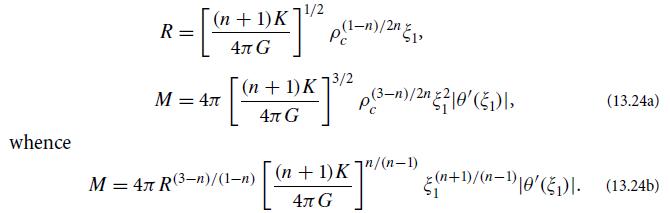
(h) When one converts a problem into dimensionless variables that satisfy some differential or algebraic equation(s) and then expresses physical quantities in terms of the dimensionless variables, the resulting expressions describe how the physical quantities scale with one another. As an example, Jupiter and Saturn are both made up of an H-He fluid that is well approximated by a polytrope of index n = 1, P = Kρ2, with the same constant K. Use the information that MJ = 2 × 1027 kg, RJ = 7 × 104 km, and MS = 6 × 1026 kg to estimate the radius of Saturn. For n = 1, the Lane-Emden equation has a simple analytical solution: θ = sin ξ/ξ. Compute the central densities of Jupiter and Saturn.
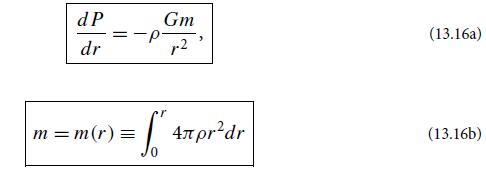
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





