Consider a system represented by the following differential equations: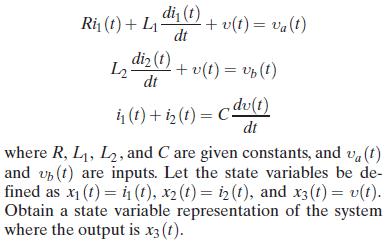

Ri(t) + Ldi (t) + v(t) = va(t) dt di (t) L2 + v(t) = vp (t) dt (t) + 2(t) = cdv(t) dt where R, L1, L2, and C are given constants, and v(t) and v(t) are inputs. Let the state variables be de- fined as x(t)=(t), x2 (t)= i2(t), and x3 (t) = v(t). Obtain a state variable representation of the system where the output is x3 (1).