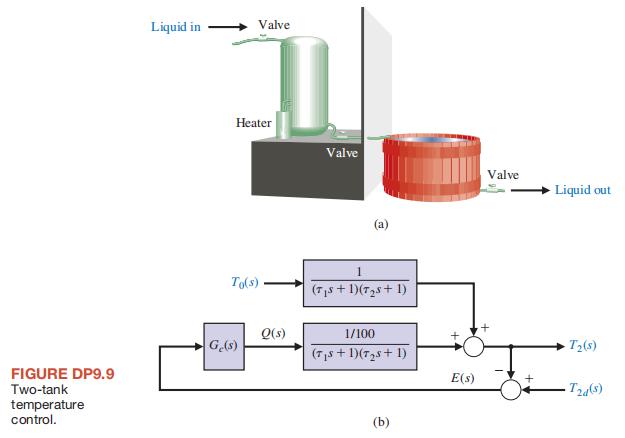
DP9.9 A two-tank system containing a heated liquid has the model shown in Figure DP9.9(a), where T0 is the temperature of the fluid flowing into the first tank and T2 is the temperature of the liquid flowing out of the second tank. The block diagram model is shown in Figure DP9.9(b). The system of the two tanks has a heater in tank 1 with a controllable heat input Q. The time constants are τ1 = 10 s and τ2 = 50 s.

(a) Determine T s 2 ( ) in terms of T s 0 ( ) and T s 2d ( ).

(b) If T s 2d ( ), the desired output temperature, is changed instantaneously from T s 2d ( ) = A s to

T s 2d ( ) = 2 , A s determine the transient response of T t 2 ( ) when G s c ( ) = = K 500. Assume that, prior to the abrupt temperature change, the sys

tem is at steady state.

(c) Find the steady-state error ess for the system of part (b), where E s( ) = − T s 2 2 d ( ) T s( ).

(d) Let G s c( ) = K s and repeat parts

(b) and (c).

Use a gain K such that the percent overshoot is

P O. . ≤ 10%.

(e) Design a controller that will result in a system with a settling time (with a 2% criterion) of Ts ≤ 150 s and a percent overshoot of P O. . ≤ 10%, while maintaining a zero steady-state error when 

(f) Prepare a table comparing the percent over

shoot, settling time, and steady-state error for the designs of parts

(b) through (e).

Gd(s) = Kp + K S