The dynamics of a controlled submarine are significantly different from those of an aircraft, missile, or surface ship. This difference results primarily from the moment in the vertical plane due to the buoyancy effect. Therefore, it is interesting to consider the control of the depth of a submarine. The equations describing the dynamics of a submarine can be obtained by using Newton’s laws and the angles defined in Figure P3.16. To simplify the equations, we will assume that θ₁(t) is a small angle and the velocity v is constant and equal to 25 ft/s. The state variables of the submarine, considering only vertical control, are x₁(t) = θ(t), x₂(t) = θ(t), and x₃(t) = a(t), where a(t) is the angle of attack. Thus the state vector differential equation for this system, when the submarine has an Albacore type hull, is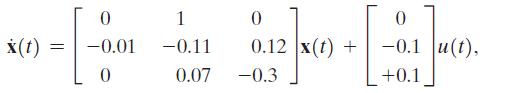where u(t) = δ_s(t), the deflection of the stern plane. 

(a) Determine whether the system is stable.
(b) Determine the response of the system to a stern plane step command of 0.285° with the initial conditions equal to zero.

x(t) = 0 -0.01 0 1 -0.11 0.07 0.12 x(t) + 12 0 -0.3 0 -0.1 u(t), +0.1